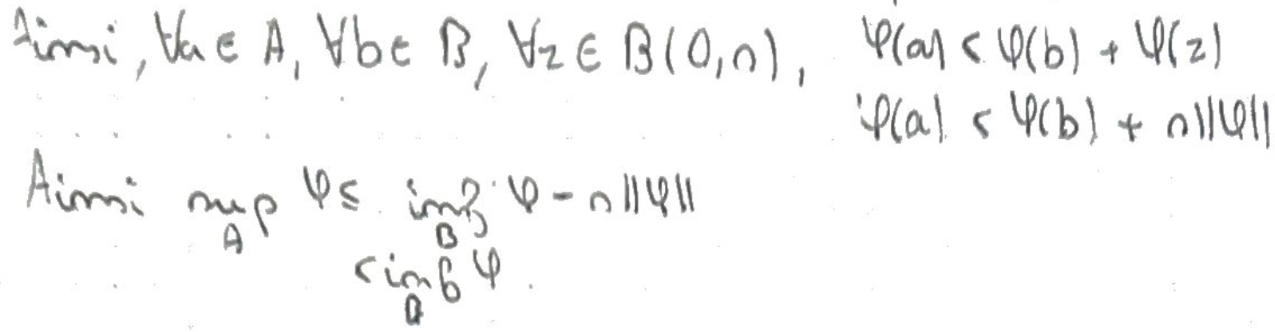On pose une suite de \(A\) et une suite de \(B\) dont la distance entre les termes tend vers \(0\).

Par Compacité, la suite de \(B\) admet une sous-suite convergente.

La suite de \(a\) converge vers la même limite, donc la limite est dans \(A\) par fermeture \(\to\) absurde.

La distance entre les deux ensembles est strictement positive.

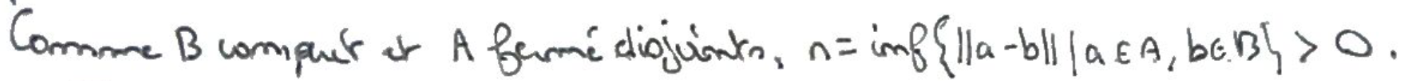
En ajoutant à \(B\) la boule centrée en \(0\) de rayon \(r\), on obtient un ensemble ouvert, toujours disjoint avec \(A\).

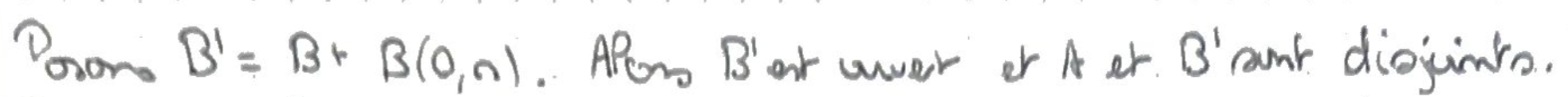
On peut donc séparer \(A\) et \(B^\prime\) par un corollaire du Théorème de séparation d'un ouvert et d'un point.

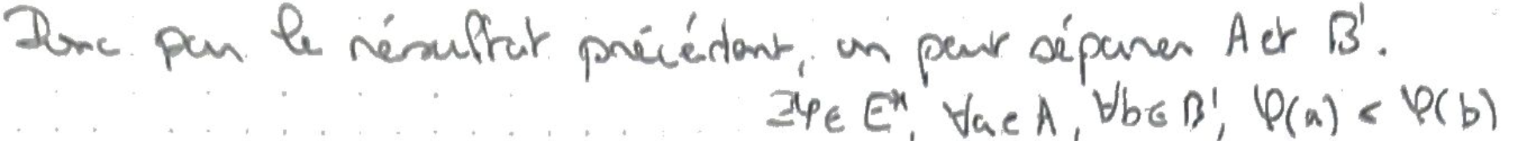
Cette séparation peut être ramenée à \(B\) par linéarité de \(\varphi\), ce qui donne le résultat voulu.

Il suffit de diviser la fonction obtenue précédemment par la moyenne entre \(\sup_A\varphi\) et \(\inf_B\varphi\).